Diuen que el professor de Gauss va manar als seus alumnes que sumessin tots els números del 1 al 100 com una forma de tenir-los callats i entretinguts. Al cap d’uns instants, per a sorpresa del professor, Gauss li va donar la resposta correcta.

Com ho va fer? La resposta… al final d’aquest article. Mentrestant, juguem a fer de Gauss!
Qui és Gauss?
Johann Carl Friedrich Gauss és un dels matemàtics més notables que ha existit.
Va fer descobertes significatives en molts camps, incloent-hi la teoria de nombres, l’estadística, l’anàlisi, la geometria diferencial, la geodèsia, l’electroestàtica, l’astronomia i l’òptica.
Fou també un nen prodigi, i hi ha moltes anècdotes respecte a la seva precocitat. I aquí comença la nostra història…

Gauss, retrat publicat a Astronomische Nachrichten (1828). Extret de Wikipedia
Un entreteniment, jugant a ser Gauss
M’entretenia sumant 1+ 2 = 3, més 4 = 10, més 5 =15, més 6 = 21, més 7 = 28… i em va cridar l’atenció que totes les sumes podien ser el resultat del producte de dos números:
- 10 = 5*2
- 15 = 5*3
- 21 = 7*3
- 28 = 7*4
- …
i que mentre un factor s’anava repetint, l’altre creixia en 1 unitat o en dues, alternativament.
Em vaig preguntar com seria la representació de la distància entre aquests números. Mans a l’obra!
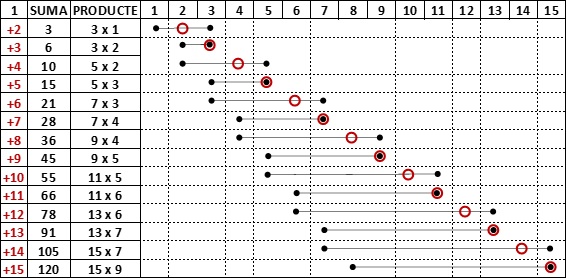
He marcat amb una rodona vermella el número que sumem. Amb uns topos negres, els dos números el producte del qual és igual a la suma.
Si observem una mica…
… podrem adonar-nos que quan sumem un número senar, aquest coincideix amb el factor més alt. Quan és parell, no.
Separant-ho per sumands parell i senars tenim:

Ara veiem clar que:
- quan sumem un número senar,
- coincideix amb el més gran dels dos factors. Per exemple, quan sumem +7, el resultat és 28, que és el resultat de 4 x 7 (el número més alt coincideix amb el que sumem)
- el factor més petit és igual a la meitat del número següent al que sumem. Per exemple, quan sumem +7, el factor més petit és (7+1)/2 = 4
- quan sumem un número parell,
- sempre és una unitat més petit que el factor més gran. Per exemple, quan sumem +8, el factor més gran és 9.
- El factor més petit és la mitat que el número que sumem. Per exemple, quan sumem +8, el factor més petit és 8/2 = 4.
Això ens permet fer un càlcul de la suma només sabent quin és el número que sumem i si és parell o senar.
Si el número ‘n’ que sumem és:
- senar, el valor de la suma serà: n x (n+1)/2
- parell, el valor de la suma serà: (n+1) x n/2
Ja tenim un mètode per calcular-ho al moment!
Però si ens hi fixem una mica, les dues fórmules són la mateixa!
- senar: n x (n+1)/2 = [n x (n+1)] / 2
- parell: (n+1) x n/2 = [(n+1) x n] / 2
O sigui, la suma d’una sèrie de números del 1 al n és la meitat del número n multiplicat pel següent: [n x (n+1)] / 2. Aquesta fórmula també la podem expressar com: (n/2) x (n+1)
Bé, resulta que hem descobert la sopa d’all! Sembla ser que aquesta fórmula és coneguda des del segle VII. Però el camí ha sigut entretingut, oi?
Com ho va resoldre Gauss?
Sembla ser que Gauss es va fixar en que si aparellava els números del començament amb els del final,
- 1+100 = 101
- 2+99 =101
- 3+98 = 101
- …
- 50+51 = 101
tenia 50 sumands de 101, o sigui 50 x 101 = 5.050, que és la resposta correcta.
Fixeu-vos que, en el fons, la formula aplicada és exactament (n/2) x (n+1) que ja hem vist, que és la fórmula que hem deduït en el nostre entreteniment.
Una altra forma de mirar-ho
Si el problema matemàtic mirem de resoldre’l visualment, ho veurem molt clar i ràpid: 50 columnes de 101. És exactament la forma en que ho va resoldre Gauss.

Historia o ficció?
Hi ha moltes versions sobre la història de Gauss i no se sap amb absoluta certesa si va ser, ni com va ser. Un article excel·lent, molt interessant i complert al respecte el trobareu a: Toda la verdad sobre la anécdota de Gauss, el niño prodigio, su profesor y la suma de 1 a 100.
© Ramon Gomà, 2022, Innovaforum



 Aqui hi ha els serveis
Aqui hi ha els serveis
